「量子コンピューターを用いた大規模なエネルギーギャップ計算手法」が米国科学アカデミー紀要（PNAS）に掲載 ～テンソルネットワークに基づいた位相推定型アルゴリズム～

　三菱ケミカル株式会社（本社：東京都千代田区、社長：筑本 学、以下「三菱ケミカル」）、慶應義塾大学（所在地：東京都港区、塾長：伊藤 公平、以下「慶大」）、ソフトバンク株式会社（本社：東京都港区、代表取締役 社長執行役員 兼 CEO：宮川 潤一、以下「ソフトバンク」）、およびJSR株式会社（本社：東京都港区、代表取締役・CEO・社長執行役員：堀 哲朗、以下「JSR」）は、慶大量子コンピューティングセンター内のIBM Q Network Hub※1にて「量子コンピューターを用いた大規模なエネルギーギャップ計算手法」を開発し、その論文が「米国科学アカデミー紀要（PNAS）」に掲載されたことをお知らせいたします。（掲載論文の URL=Tensor-based quantum phase difference estimation for large-scale demonstration | PNAS）。

【本研究のポイント】
・エネルギーギャップ計算手法である量子位相差推定とテンソルネットワークによる回路圧縮技術を組み合わせた「テンソルに基づく位相差推定（TQPDE）」を開発
・大規模分子に対する物性の高解像度な理解への期待

　今回、大規模な分子のエネルギーギャップを高精度で求めるために、エネルギーギャップの計算手法のひとつである量子位相差推定とテンソルネットワークによる量子回路圧縮を組み合わせた手法を提案し、この手法をゲート型商用量子コンピューター「IBM Quantum System One」および「IBM Quantum System Two」上で、ハバードモデルおよび直鎖分子に対して実行しました。Q-CTRL社のエラー抑制モジュールを組み合わせることで、従来の5倍以上である最大32量子ビット（32スピン軌道）のシステムに対するエネルギーギャップの計算に成功しました。
　この結果は、大規模な分子の物性を高精度に解析する道を切り拓くことが期待されます。

　三菱ケミカル、慶大、ソフトバンクおよびJSRは、今後も材料開発をはじめとする、量子コンピューターを用いた幅広い実応用の技術確立に向けて取り組んでまいります。

※1：慶大とIBMが2018年5月に慶大理工学部に開設した最先端の量子コンピューター研究拠点です。
IBM が開発した最先端の量子コンピューターのクラウド利用を可能とするアジア初の IBM Quantum Hubであり、産学共同の研究拠点として三菱ケミカルは発足メンバーとして参画しています。

以上

ご参考

【背景】
　分子の物性は、物質に含まれる電子の状態を計算することで知ることができます。しかし、電子状態の計算は電子の数に応じて指数的にコストが増加するため、現状は近似を利用して計算を行います。電子の基底状態※2の計算では、電子相関を近似したDFT※3が広く用いられますが、クーロン反発が強い複雑な電子構造を持つ物質の場合、十分な精度が得られないという課題があります。

　量子コンピューターは量子もつれ※4と重ね合わせ※5により、従来（古典）コンピューターでは実行できないような計算が可能であるため、この課題の解決策として注目されています。代表的なアルゴリズムである量子位相推定では分子のエネルギーを指数的に高速化できるとされています。しかし現在の量子コンピューターはノイズが多く、大規模な量子回路※6を実行することができないため、量子位相推定は最大でも6ビットのシステムまでしか実行されていませんでした。

【今回の成果】
　本研究では量子計算における計算コストを削減するために、量子位相差推定とテンソルネットワーク※7を採用しました。量子位相差推定では基底状態と励起状態※8の重ね合わせ状態を用いることで、重要な物性値であるエネルギーギャップを直接計算することができます。また、通常の量子位相推定[図1(a)]と位相差推定[図1(b)]の回路を比較すると、ダイナミクス計算exp(-iHt)における補助ビットの制御演算を回避しており、計算コストを削減できることもポイントです。

　この量子位相差推定回路をベースに、テンソルネットワークと呼ばれる技術を用いることでさらに回路を圧縮しました[図1(c)]。この技術では、目的の回路を近似するような浅い回路を古典コンピューターで探索します。また副次効果として、テンソルネットワークによる状態準備回路の実装はノイズを指数的に抑える効果があることも分かりました。

　この手法を32システム量子ビットのハバードモデル[図2(a)]と、20量子ビットのデカペンタエン[図2(b)]において実機実行しました。この際、Q-CTRL社のエラー抑制モジュールを併用することで、さらなる回路圧縮を行っており、標準トランスパイルでは7242の制御Zゲートが必要であった回路を794まで圧縮することができました。その結果、目標となるエネルギーギャップ値への測定分布の収縮が見られ、アルゴルズムが正しく動作することが確認できました（精度は10ミリハートリーのオーダー）。これは、従来の5倍以上の規模で量子位相推定型アルゴリズムが動作したことになります。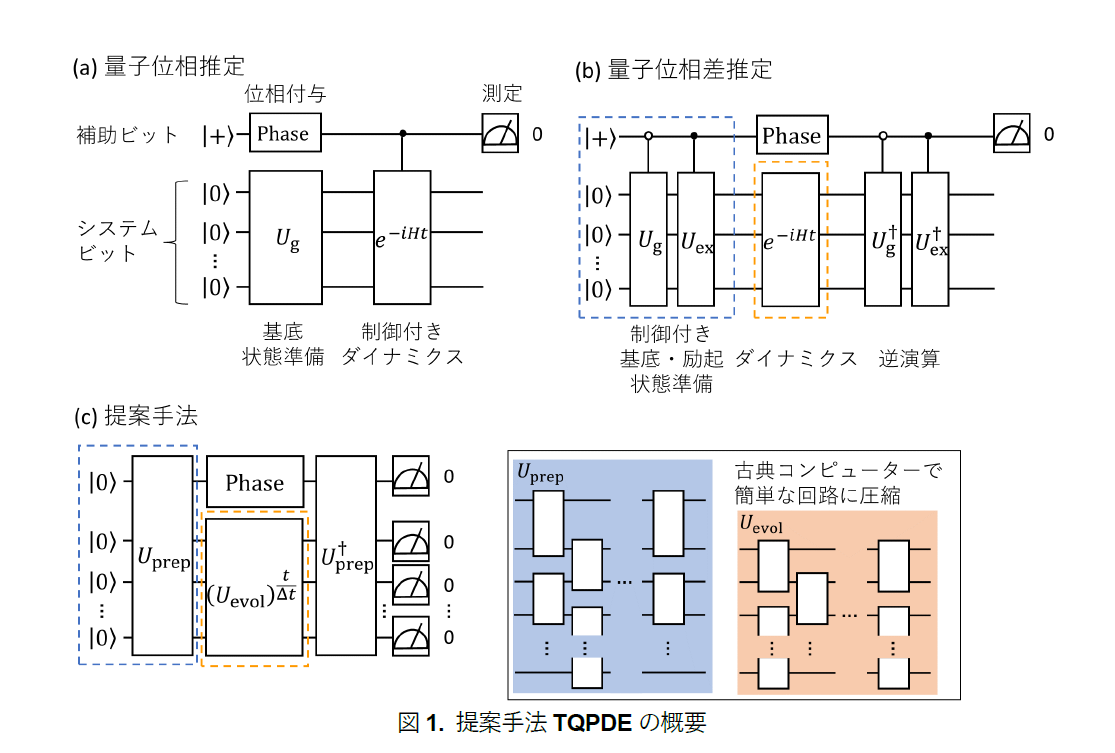

(a) 量子位相推定（ベイズ型）の回路図。最上のビットが補助量子ビットでそれ以外がシステムに対応する量子ビットです。Ugで近似基底状態を準備し、Phaseで位相を付与し、制御付きダイナミクスexp(-iHt)を実行し、最後に補助ビットを測定します。X測定で0が測定される確率が位相によって（コサイン関数の形で）変化し、位相が基底状態エネルギーと一致する時に確率ピークをとります。ダイナミクスの時間tを変化させることでピーク幅を変化させ、イタレーションごとにエネルギー値を絞りこんでいきます。

(b) 量子位相差推定の回路図。エネルギー絶対値の代わりに、二準位間のエネルギーギャップを計算します。それに合わせて基底と励起状態を準備するための制御付き準備回路（それぞれUg, Uex）を準備します。状態準備回路が制御付きになっている代わりにダイナミクスの制御がなくなっており、計算コストが下がります（一般に状態準備の方がダイナミクスより簡単です）。

(c) 提案手法の回路図。テンソルネットワークを用いて状態準備回路とダイナミクス回路を古典コンピューターで近似的に圧縮した回路を取得します（それぞれUprepとUevol）。古典コンピューターで効率的に計算できるのは短時間のダイナミクスのため、まず短時間Δtのダイナミクス演算を古典コンピューターで圧縮してUevolを作成したのち、それをt/Δt回重ねることで、量子回路上で長時間のダイナミクスを実行します。測定では全ビットのZ測定で0が得られた確率を利用します。この測定により、ノイズが指数的に抑制されます。

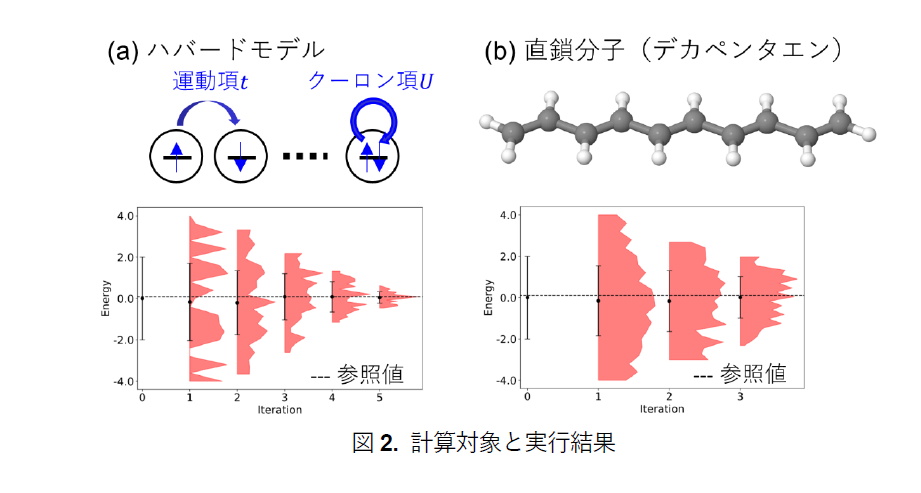
(a) ハバードモデル。ハバードモデルは電子の相関を取り扱うシンプルなモデルで、運動エネルギー項tとクーロンエネルギー項Uから構成されます。下側は計算結果（32ビットシステム）です。赤色の分布が位相の値ごとにサンプルされた確率分布で、分布のピークがエネルギーギャップに相当します。横軸のイタレーションが増加するほどダイナミクスの計算時間が伸び、分布（つまりコサイン関数の周期）が狭まります。イタレーションごとに分布が参照となるギャップ値（破線）に収束する様子が見られ、提案手法が実機でも動作することが確認されました。
(b) 直鎖分子。分子システムはハバードモデルよりも相互作用が複雑ですが、軌道の局在化処理を行うことで、20システムビットのデカペンタエンの実行ができました。
【今後の展望】
量子位相推定は、化学計算にとどまらず、素因数分解や機械学習など幅広いタスクに適用可能な、最も代表的な量子コンピューターのアルゴリズムの一つです。これまで、量子位相推定は古典コンピューターで容易に検証可能な数ビット規模のトイモデルにとどまっていましたが、今回の研究により、古典コンピューターの限界に迫る大規模な系への適用が可能となりました。これにより、量子コンピューターによる実用化に向けた歩みが大きく前進したといえます。
【用語解説】
※2：基底状態
最もエネルギーの低い電子状態。
※3：DFT
密度汎関数(density functional theory)法の略。
※4：量子もつれ
量子ビットが複数の状態を同時にとる性質。
※5：量子重ね合わせ
複数の量子ビット間で状態が相互に依存している関係。
※6：量子回路
量子ビットの量子状態を制御する量子ゲートや測定を組み合わせたもの。
※7：テンソルネットワーク
テンソルは、スカラー（0次元）、ベクトル（1次元）、行列（2次元）を一般化したもので、任意の次元を持つデータ構造。テンソルネットワークは、テンソルをグラフ構造で接続したもの。今回は量子ゲートなどをテンソルとして扱う。
※8：励起状態

基底状態よりエネルギーの高い電子状態。

＜共著者リスト＞
・三菱ケミカル株式会社 ：菅野 志優、小林 高雄、高 玘
・慶應義塾大学 ：杉崎 研司（当時）、中村 肇、山本 直樹
・ソフトバンク株式会社 ：山内 啓嗣
・JSR株式会社 ：佐久間 怜

【参考プレスリリース】
・「光機能性物質のエネルギーを求めるための量子コンピューターを用いた新たな計算手法」が Nature Research 出版社の専門誌に掲載（2023年2月9日）
・有機 EL 発光材料性能予測に関する研究成果が Nature 専門誌に掲載（2021年5月26日）
・「量子コンピューターを用いた大規模な分子・固体向け高精度エネルギー計算手法」がNature Research 出版社の専門誌に掲載（2024年6月10日）
以上